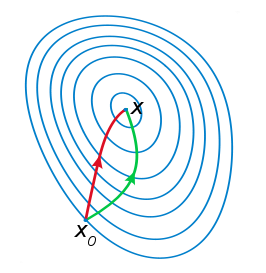
梯度下降法

梯度下降法是学习机器学习的线性回归最先遇到的优化算法。对损失函数，求其梯度，找到下降最快的方向。

梯度下降法的算法流程如下：

首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。
改变θ的值，使得J(θ)按梯度下降的方向进行减少。

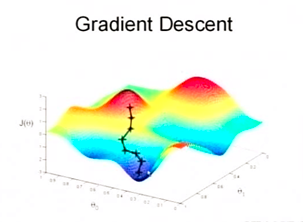
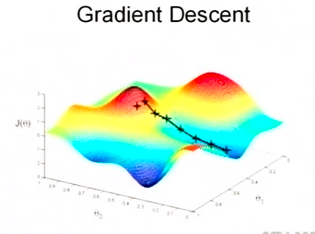
梯度下降法需要注意的是，除了二次凸优化问题可以确定找到全局唯一最小解。对于其他的情况，找到的可能是一个局部最小点。因此初值的选择很重要，可以通过多次选择初值的方式，避免陷入局部最小点。

牛顿法

牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。牛顿法最大的特点就在于它的收敛速度很快。
具体步骤：
首先，选择一个接近函数 f(x)零点的x0，计算相应的 f(x0) 和切线斜率f'(x0)（这里f’表示函数f的导数）。然后我们计算穿过点(x0, f(x0)) 并且斜率为f'(x0)的直线和 x 轴的交点的x坐标，也就是求如下方程的解：

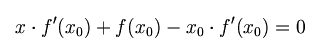
我们将新求得的点的 x 坐标命名为x1，通常x1会比x0更接近方程f(x) = 0的解。因此我们现在可以利用x1开始下一轮迭代。迭代公式可化简为如下所示：

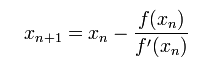
已经证明，如果f’是连续的，并且待求的零点x是孤立的，那么在零点x周围存在一个区域，只要初始值x0位于这个邻近区域内，那么牛顿法必定收敛。并且，如果f ‘ (x)不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说，这意味着每迭代一次，牛顿法结果的有效数字将增加一倍。
由于牛顿法是基于当前位置的切线来确定下一次的位置，所以牛顿法又被很形象地称为是”切线法”。

关于牛顿法和梯度下降法的效率对比

从收敛速度上看，牛顿法是二阶收敛，梯度下降是一阶收敛，前者牛顿法收敛速度更快。但牛顿法仍然是局部算法，只是在局部上看的更细致，梯度法仅考虑方向，牛顿法不但考虑了方向还兼顾了步子的大小，其对步长的估计使用的是二阶逼近。
根据wiki上的解释，从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

梯度下降法是一阶收敛的，牛顿法是二阶收敛的。